Clustered sparsity and Poisson-gap sampling

Kasprzak, P.; Urbańczyk, M.; Kazimierczuk, K.

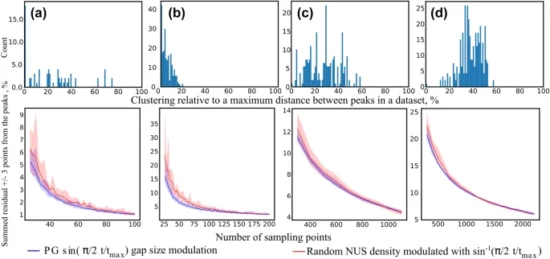
Non-uniform sampling (NUS) is a popular way of reducing the amount of time taken by multidimensional NMR experiments. Among the various non-uniform sampling schemes that exist, the Poisson-gap (PG) schedules are particularly popular, especially when combined with compressed-sensing (CS) reconstruction of missing data points. However, the use of PG is based mainly on practical experience and has not, as yet, been explained in terms of CS theory. Moreover, an apparent contradiction exists between the reported effectiveness of PG and CS theory, which states that a “flat” pseudo-random generator is the best way to generate sampling schedules in order to reconstruct sparse spectra. In this paper we explain how, and in what situations, PG reveals its superior features in NMR spectroscopy. We support our theoretical considerations with simulations and analyses of experimental data from the Biological Magnetic Resonance Bank (BMRB). Our analyses reveal a previously unnoticed feature of many NMR spectra that explains the success of ”blue-noise” schedules, such as PG. We call this feature “clustered sparsity”. This refers to the fact that the peaks in NMR spectra are not just sparse but often form clusters in the indirect dimension, and PG is particularly suited to deal with such situations. Additionally, we discuss why denser sampling in the initial and final parts of the clustered signal may be useful.